라떼는말이야
[solved.ac 골드4] 1717_집합의 표현 (파이썬, union-find). Union-Find 자세한 설명 본문
[solved.ac 골드4] 1717_집합의 표현 (파이썬, union-find). Union-Find 자세한 설명
MangBaam 2022. 8. 20. 18:17https://github.com/mangbaam/CodingTest
GitHub - mangbaam/CodingTest: 프로그래머스, 백준 등 코딩테스트 풀이를 기록하는 저장소입니다.
프로그래머스, 백준 등 코딩테스트 풀이를 기록하는 저장소입니다. Contribute to mangbaam/CodingTest development by creating an account on GitHub.
github.com
밑의 사진을 클릭하면 문제 링크로 이동합니다



문제
초기에 {0}, {1}, {2}, ... {n} 이 각각 n+1개의 집합을 이루고 있다. 여기에 합집합 연산과, 두 원소가 같은 집합에 포함되어 있는지를 확인하는 연산을 수행하려고 한다.
집합을 표현하는 프로그램을 작성하시오.
입력
첫째 줄에 n(1 ≤ n ≤ 1,000,000), m(1 ≤ m ≤ 100,000)이 주어진다. m은 입력으로 주어지는 연산의 개수이다. 다음 m개의 줄에는 각각의 연산이 주어진다. 합집합은 0 a b의 형태로 입력이 주어진다. 이는 a가 포함되어 있는 집합과, b가 포함되어 있는 집합을 합친다는 의미이다. 두 원소가 같은 집합에 포함되어 있는지를 확인하는 연산은 1 a b의 형태로 입력이 주어진다. 이는 a와 b가 같은 집합에 포함되어 있는지를 확인하는 연산이다. a와 b는 n 이하의 자연수 또는 0이며 같을 수도 있다.
출력
1로 시작하는 입력에 대해서 한 줄에 하나씩 YES/NO로 결과를 출력한다. (yes/no 를 출력해도 된다)
예제
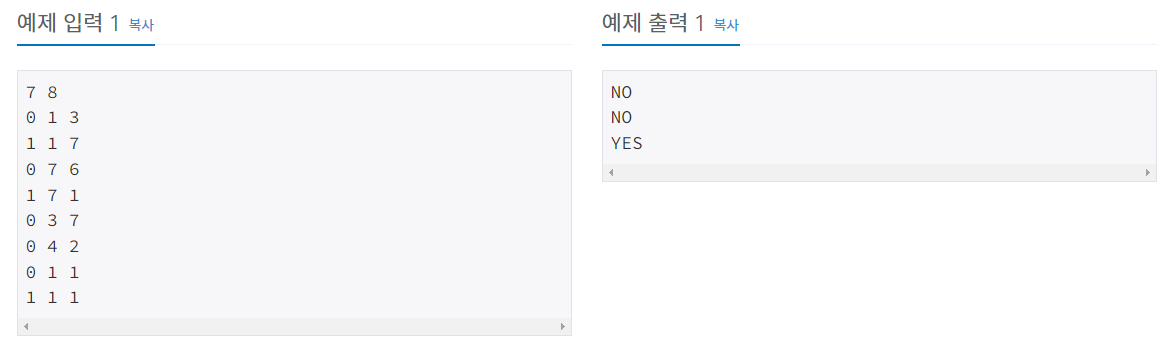
나의 풀이
문제 자체가 Union Find 알고리즘을 나타내고 있다. union-find 알고리즘은 자체적인 알고리즘인지만 크루스칼 알고리즘에서도 사용하는 걸로 유명하다.
Union Find 알고리즘은 Union 기능과 Find 기능을 가지고 있으며 Union 은 두 집합을 하나의 집합으로 합치는 역할을 하고, Find 는 집합의 대표 노드(주로 트리 구조에서 루트 노드)를 찾아서 반환하는 역할을 한다.
시간 복잡도를 줄이기 위해 여러 방법이 사용되는데 대표적으로 Find 하는 과정 중 Path Compression 이 있다.
Find
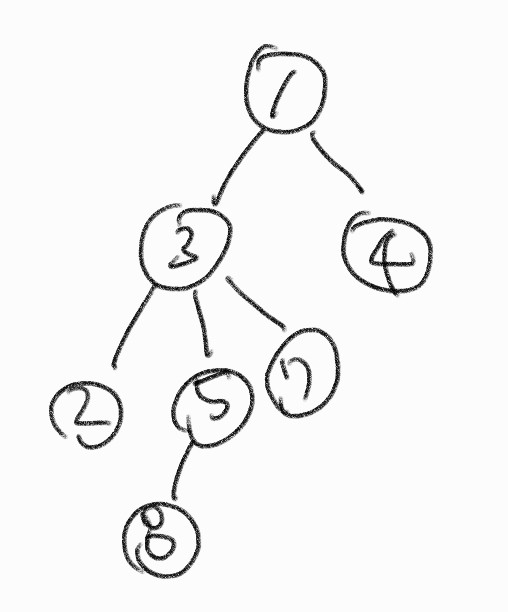
위와 같은 트리가 있을 때 연결된 모든 노드들은 하나의 그룹이라고 표현할 수 있다.
그리고 find() 함수는 특정 노드가 어떤 그룹에 속해있는지 판별하기 위해 사용되는데 주로 트리 구조에서 루트 노드를 반환한다.
위 트리에서 find(8) 을 하게 되면 1을 반환해야 한다.
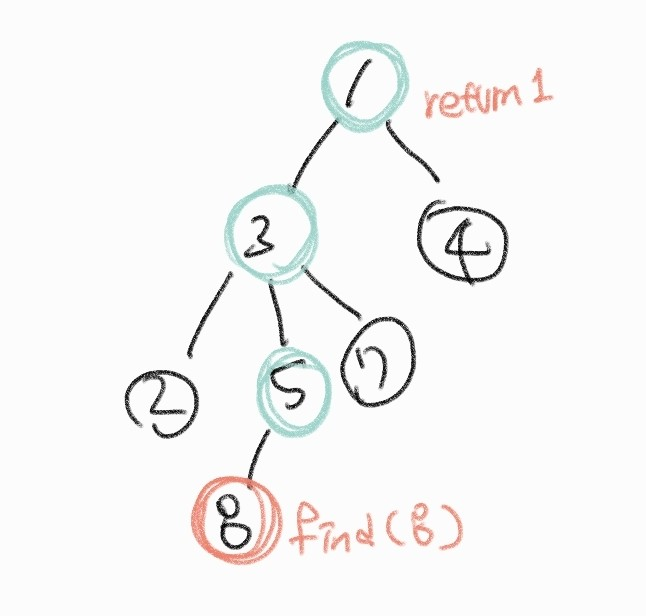
이 과정은 재귀적으로 부모 노드를 탐색하며 거슬러 올라가면서 찾게 된다. 루트 노드는 부모 노드로 자기 자신을 가리키고 있기 때문에 parent[node] == node 와 같은 방법으로 루트 노드임을 확인하게 된다.
Path compression
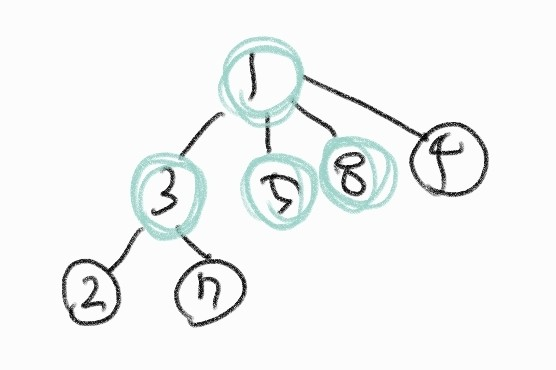
find 과정에서 Path compression 기법을 사용할 수 있다. Path compression은 트리의 구조를 변경시켜 시간 복잡도를 줄이는 기법인데 그 결과 위와 같은 트리 구조가 된다.
8부터 탐색해서 거쳐가는 모든 노드들이 루트 노드를 가리키는 구조로 변경된다.
이렇게 구조를 바꾸어나가면 한 번만 거슬러 올라가면 되기 때문에 O(1) 에 맞먹는 속도까지 단축될 수 있다. (완전 상수 시간은 아니지만 x가 2^65536 만큼의 크기일 때 5 만큼의 연산을 한다고 하니 상수시간에 맞먹는다고 표현했다 - 애커만 함수)
# path compression 적용 안 됨
def find(node):
if parent[node] == node:
return node
else:
return find(parent[node])
# path compression 적용 됨
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]경로 압축이 적용된 코드를 보면 parent 값을 재귀적으로 호출할 때마다 가리키면서 결국 모두 루트 노드를 가리키도록 하고 있다.
Union
Union 은 두 집합을 하나의 집합으로 합친다. 트리 구조로 되어 있을 때 두 트리를 하나의 트리로 합치는 것이다.
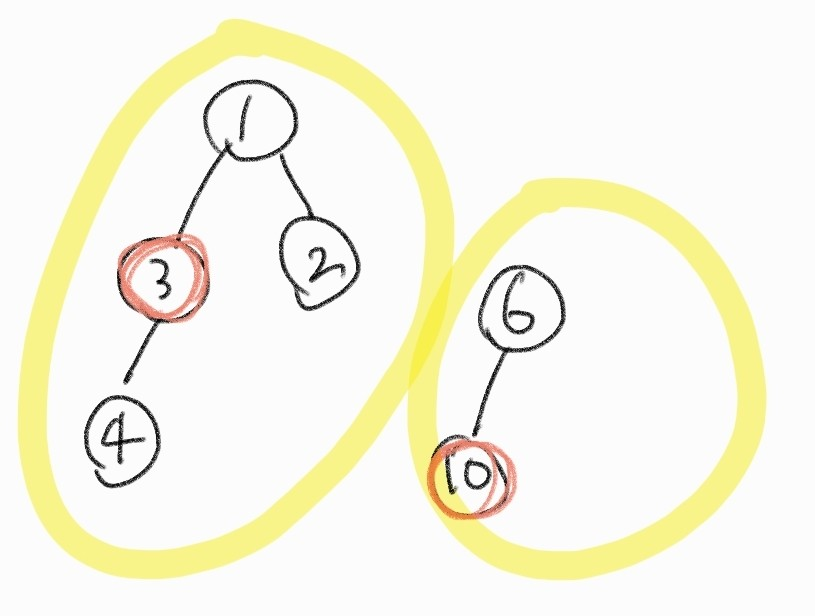
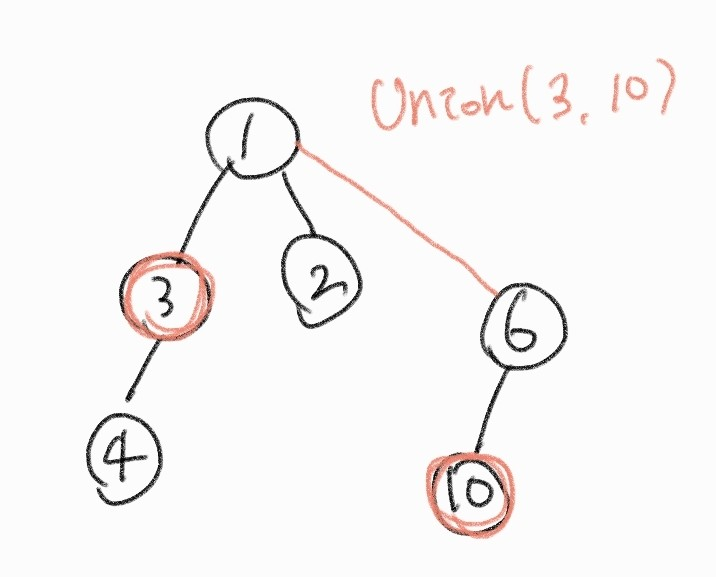
왼쪽 그림과 같이 2 개의 트리가 있고, union(3, 10) 을 했을 때 노드3과 노드10이 포함된 각각의 루트 노드를 찾아 한 쪽의 루트 노드를 다른 쪽의 루트 노드에 연결해주는 방식으로 union 이 진행된다.
그리고 루트 노드를 찾는 과정에서 위에서 설명한 Find 함수를 사용한다.
def union(node1, node2):
root1, root2 = find(node1), find(node2)
parent[root2] = root1보통 다른 곳에서 설명하는 것을 보면 보통은 위와 같은 방식으로 진행한다. 두 번째 트리를 첫 번째 트리에 연결하는 방식이다.
하지만 이 방법에서도 시간 복잡도를 줄일 수 있는 좋은 방법이 있다.
바로 rank 를 사용하는 방법이다. (rank 란 트리의 높이를 의미한다)
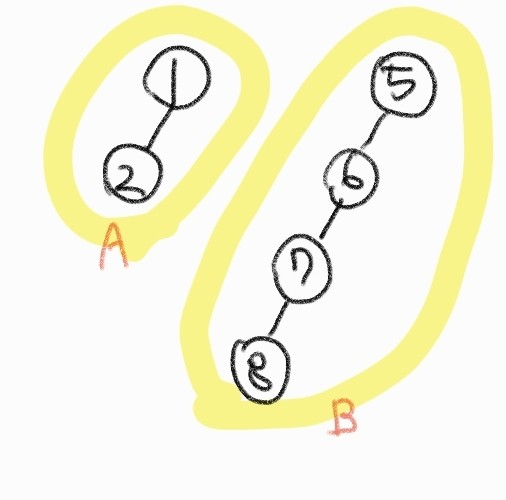
위 그림과 같이 2 개의 그룹(트리)가 있다고 해보자. 그리고 union 을 할 때 A 에 B 를 연결하거나 반대로 B 에 A 를 연결하는 두 개의 선택지가 있을 것이다.
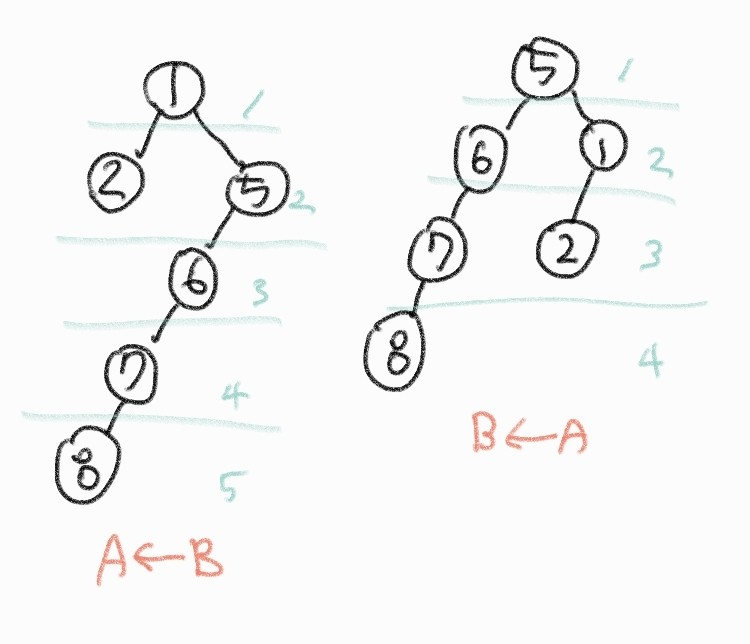
두 개 다 살펴보면 union 의 결과 트리의 rank 가 다르다. 어떤 트리에 붙이냐에 따라 효율적이지 않은 결과를 만들어 낼 수 있다.
해결 방법은 간단하다.
rank 가 낮은 tree 를 rank 가 높은 tree 에 연결하면 된다.

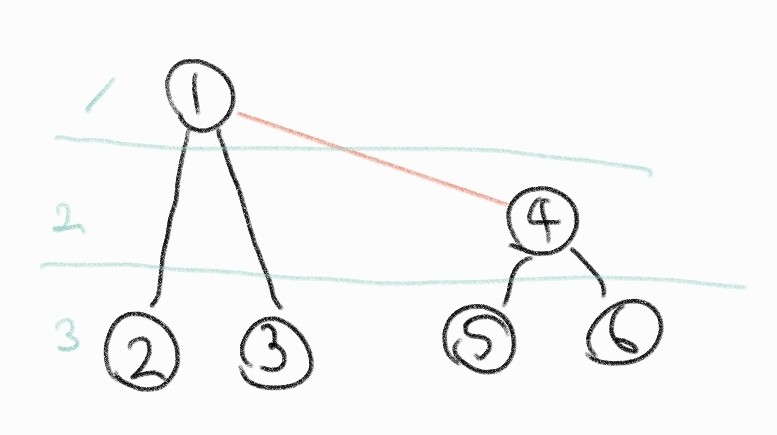
만약 왼쪽 그림과 같이 랭크가 같은 트리를 합치는 경우엔 오른쪽 그림처럼 연결하고 rank 를 높이면 된다.
def union(a, b):
p1, p2 = find(a), find(b)
if rank[p1] > rank[p2]:
parent[p2] = p1
else:
parent[p1] = p2
if rank[p1] == rank[p2]:
rank[p2] += 1전체 코드
import sys
def input():
return sys.stdin.readline().rstrip()
n, m = map(int, input().split())
parent = list(range(n + 1)) # 초기에 모두 자기 자신을 가리킴
rank = [1] * (n + 1) # 초기 rank 는 모두 1
def find(x):
if parent[x] != x:
parent[x] = find(parent[x]) # path compression
return parent[x]
def union(a, b):
p1, p2 = find(a), find(b)
if rank[p1] > rank[p2]: # union by rank
parent[p2] = p1
else:
parent[p1] = p2
if rank[p1] == rank[p2]:
rank[p2] += 1
same = lambda a, b: find(a) == find(b) # check same group
for _ in range(m):
a, b, c = map(int, input().split())
if a:
print("YES") if same(b, c) else print("NO")
else:
union(b, c)
'알고리즘 > 코딩 테스트' 카테고리의 다른 글
| [solved.ac 골드3] 9944_NxM 보드 완주하기 (파이썬, 백트래킹) (0) | 2022.09.16 |
|---|---|
| [solved.ac 골드4] 전생했더니 슬라임 연구자였던 건에 대하여 (Hard) (파이썬, 우선순위 큐, 그리디, 수학) (0) | 2022.08.28 |
| [solved.ac 골드2] 1167_트리의 지름 (파이썬, BFS) (0) | 2022.08.20 |
| [solved.ac 골드1] 11003_최솟값 찾기 (파이썬, 슬라이딩 윈도우) (0) | 2022.08.19 |
| [solved.ac 골드3] 10986_나머지 합 (파이썬) (0) | 2022.08.19 |
| [프로그래머스 lv3] 순위 (코틀린, 플로이드-워셜) (0) | 2022.08.19 |
| [프로그래머스 lv3] 가장 먼 노드 (다익스트라, 코틀린) (0) | 2022.08.18 |
| [solved.ac 골드5] 17396_백도어 (다익스트라, 코틀린) (0) | 2022.08.16 |




