라떼는말이야
[프로그래머스 lv3] 순위 (코틀린, 플로이드-워셜) 본문
https://github.com/mangbaam/CodingTest
GitHub - mangbaam/CodingTest: 프로그래머스, 백준 등 코딩테스트 풀이를 기록하는 저장소입니다.
프로그래머스, 백준 등 코딩테스트 풀이를 기록하는 저장소입니다. Contribute to mangbaam/CodingTest development by creating an account on GitHub.
github.com
밑의 사진을 클릭하면 문제 링크로 이동합니다


문제
n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다. 권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다. 심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.
선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
- 선수의 수는 1명 이상 100명 이하입니다.
- 경기 결과는 1개 이상 4,500개 이하입니다.
- results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
- 모든 경기 결과에는 모순이 없습니다.
입출력 예

나의 풀이
백준에서 비슷한 문제를 풀어봐서 쉽게 돌파구를 찾을 수 있었다.
모든 노드로부터 최단 거리를 찾기 위한 알고리즘으로 유명한 플로이드-워셜 알고리즘을 사용해서 풀이했다. 최단 거리를 찾을 때는 큰 값으로 초기화 한 후 줄여나가는 방식이지만 이 문제나 위에서 언급한 백준 문제와 같이 어떠한 사건의 순서를 찾기 위해서도 플로이드-워셜 알고리즘이 사용되고, 이때는 큰 값으로 초기화 하는 것이 아닌 false 로 초기화 한 후 진행하게 된다.
플로이드 워셜 알고리즘에 대해서 알고 있다는 가정 하에 다음 설명을 이어나가려고 한다.
class Solution {
fun solution(n: Int, results: Array<IntArray>): Int {
val graph = Array(n + 1) { BooleanArray(n + 1) }
results.forEach { (a, b) ->
graph[a][b] = true
}
// floyd-warshall 알고리즘
for (k in 1..n) {
for (x in 1..n) {
for (y in 1..n) {
if (graph[x][k] && graph[k][y]) {
graph[x][y] = true
}
}
}
}
// ...
}선수 번호가 1번 부터 시작하기 때문에 Array 를 n + 1 크기로 만들었고, results 각각에 대해 graph 에 true 로 값을 반영해주는 초기화 과정을 거친 후 플로이드 워셜 알고리즘을 수행한다.
graph[x][k] 가 true 이고 graph[k][y] 가 true 일 때 graph[x][y] 를 true 로 설정하는 것은 x 가 k 를 이기고, k 가 y 를 이기면 x 는 y 를 이기기 때문이다.
위 과정을 완료하면 누가 누구를 이길 수 있는지 알 수 있다.
하지만 문제에서 요구한 것은 순위가 확실한 선수의 수였다.
이건 간단하다.
2번 선수의 순위가 확실한지 확인하려면 1, 3, 4, 5 선수와의 결과가 서로 상반되어야 한다.
예를 들어 graph[2][1] 이 true 면 2번 선수가 1번 선수를 이긴다는 것이라서 graph[1][2] 는 false 여야 한다. 하지만 graph 는 true 와 false 둘 중 하나의 값만 가질 수 있기 때문에 두 선수의 승부가 확실하지 않다면 둘 다 true 이거나 false 일 수 있다.
하지만 자신을 제외한 모든 선수가 결과가 상반된다면 순위가 확실한 것이기 때문에 개수를 세면 된다.
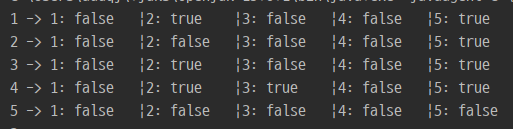
위 사진은 플로이드 워셜 알고리즘 수행 후 graph 를 출력한 것이다. (의미 없는 0번 인덱스는 제외했다)
1번 선수를 보면 3번 선수를 이긴다고 했지만 3번 선수도 1번 선수를 이긴다고 되어 있으니 승부가 확실하지 않은 것이다.
반면 2번 선수를 보면 1번, 3번, 4번, 5번 선수와의 결과가 모두 상반되기 때문에 5번 선수만 이긴다는 것이 확실하다.
5번 선수도 마찬가지로 자신을 제외한 모든 선수와 결과가 상반되기 때문에 모든 선수에게 패배한 사실이 확실하다.
// ...
var count = 0
var flag: Boolean
graph.drop(1).forEachIndexed { i, it ->
flag = true
it.drop(1).forEachIndexed { j, b ->
if (i != j && !(graph[i + 1][j + 1] xor graph[j + 1][i + 1])) flag = false
}
if (flag) count++
}
return count
}조건문을 보면 xor 로 서로 상반되는 결과를 가지고 있는지 확인하고 있다. flag 를 세워서 한 번이라도 같은 결과가 나온다면 flag 를 false 로 설정해 count 가 증가되지 않도록 했다.
모든 선수와 결과가 상반된 경우만 count 가 증가하므로 count 에는 순위가 확실한 선수의 수가 들어있게 된다.
전체 코드
class Solution {
fun solution(n: Int, results: Array<IntArray>): Int {
val graph = Array(n + 1) { BooleanArray(n + 1) }
results.forEach { (a, b) ->
graph[a][b] = true
}
for (k in 1..n) {
for (x in 1..n) {
for (y in 1..n) {
if (graph[x][k] && graph[k][y]) {
graph[x][y] = true
}
}
}
}
var count = 0
var flag: Boolean
graph.drop(1).forEachIndexed { i, it ->
flag = true
it.drop(1).forEachIndexed { j, b ->
if (i != j && !(graph[i + 1][j + 1] xor graph[j + 1][i + 1])) flag = false
}
if (flag) count++
}
return count
}
}
'알고리즘 > 코딩 테스트' 카테고리의 다른 글
| [solved.ac 골드4] 1717_집합의 표현 (파이썬, union-find). Union-Find 자세한 설명 (0) | 2022.08.20 |
|---|---|
| [solved.ac 골드2] 1167_트리의 지름 (파이썬, BFS) (0) | 2022.08.20 |
| [solved.ac 골드1] 11003_최솟값 찾기 (파이썬, 슬라이딩 윈도우) (0) | 2022.08.19 |
| [solved.ac 골드3] 10986_나머지 합 (파이썬) (0) | 2022.08.19 |
| [프로그래머스 lv3] 가장 먼 노드 (다익스트라, 코틀린) (0) | 2022.08.18 |
| [solved.ac 골드5] 17396_백도어 (다익스트라, 코틀린) (0) | 2022.08.16 |
| [solved.ac 실버2] 18352_특정 거리의 도시 찾기 (다익스트라, 코틀린) (0) | 2022.08.16 |
| 코틀린 다익스트라 알고리즘 Kotlin dijkstra algorithm (0) | 2022.08.16 |




