라떼는말이야
[프로그래머스 lv3] 등굣길 (DP 풀이) 본문

문제 설명
계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.
아래 그림은 m = 4, n = 3 인 경우입니다.

가장 왼쪽 위, 즉 집이 있는 곳의 좌표는 (1, 1)로 나타내고 가장 오른쪽 아래, 즉 학교가 있는 곳의 좌표는 (m, n)으로 나타냅니다.
격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.
제한사항
- 격자의 크기 m, n은 1 이상 100 이하인 자연수입니다.
- m과 n이 모두 1인 경우는 입력으로 주어지지 않습니다.
- 물에 잠긴 지역은 0개 이상 10개 이하입니다.
- 집과 학교가 물에 잠긴 경우는 입력으로 주어지지 않습니다.
입출력 예

입출력 예 설명

나의 풀이
이 문제는 DP로 풀이할 수 있다. (DP 외에 BFS 등의 알고리즘으로도 풀이할 수 있을 것으로 생각된다)
1. 그래프로 표현
def solution(m, n, puddles):
answer = 0
d = [[10e+9] * n for _ in range(m)]
for puddle in puddles:
d[puddle[0]-1][puddle[1]-1] = 'x'파이썬에서 이중리스트는 list[행][열]의 순으로 접근할 수 있다. 하지만 문제에서는 m: 열, n: 행으로 주어졌다. 나는 내가 평소 사용하던 방식대로 list[행][열]의 순으로 접근하고자 m: 행, n: 열로 변경했다.
d라는 변수에 n x m 크기의 이중리스트를 선언하고, 10e+9로 초기화하였다. 10e+9는 10000000000.0 이므로 충분히 큰 값을 표현할 수 있다.
그리고 puddles를 순회하며 물 웅덩이를 'x'로 나타냈다.
2. 최단 거리로 학교에 가는 방법
집은 항상 왼쪽 위에 있고, 학교는 항상 오른쪽 아래에 있다.
최단 거리로 학교에 갈 수 있는 방법은 왼쪽이나 위로 돌아오지 않고 무조건 오른쪽 혹은 아래 방향으로 이동하는 것이다. (대각선으로는 이동 불가)
3. 첫 열 초기화
def solution(m, n, puddles):
answer = 0
# ...
# 1. 물웅덩이 초기화
# 3. 첫 열 초기화
for i in range(1, n):
if d[0][i] == 'x' or d[0][i-1] == 'x': d[0][i] = 'x'
else: d[0][i] = 1집에서부터 무조건 오른쪽으로만 가면 최단 거리로 학교에 갈 수 있는 경로 중 하나가 된다.
이때 만약 첫 열에 물 웅덩이가 있다면 물 웅덩이가 있는 곳 이후부터는 모두 최단 거리로 갈 수 없게 된다. 왜냐하면 물 웅덩이를 피해 가려면 아래로 갔다가 다시 위로 올라가야 하기 때문에 최단 거리가 될 수 없다.
그래서 첫 열을 초기화 하는 중에 물 웅덩이를 만나면 그 이후의 남은 칸은 모두 물 웅덩이와 같이 취급한다.
그 외에는 1로 초기화한다. 최단 경로가 단 하나만 존재하기 때문이다.
4. 첫 행 초기화
def solution(m, n, puddles):
answer = 0
# ...
# 1. 물웅덩이 초기화
# 3. 첫 열 초기화
for i in range(1, n):
if d[0][i] == 'x' or d[0][i-1] == 'x': d[0][i] = 'x'
else: d[0][i] = 1
# 4. 첫 행 초기화
for j in range(1, m):
if d[j][0] == 'x' or d[j-1][0] == 'x': d[j][0] = 'x'
else: d[j][0] = 13번의 첫 열 초기화와 같은 이유로 첫 행을 초기화한다.
5. 계산
def solution(m, n, puddles):
answer = 0
# ...
# 1. 물웅덩이 초기화
# 3. 첫 열 초기화
# 4. 첫 행 초기화
# ...
for x in range(1, m):
for y in range(1, n):
# 현재 위치가 x이거나 왼쪽, 윗칸 모두 x라면 계산 불가
if d[x][y] == 'x' or (d[x-1][y], d[x][y-1]) == ('x','x'): continue
# 윗칸이 x이거나 초기값이라면 왼쪽 값 그대로 사용
if d[x-1][y] in ('x', 10e+9): d[x][y] = d[x][y-1]
# 왼쪽 칸이 x이거나 초기값이라면 윗쪽 값 그대로 사용
elif d[x][y-1] in ('x', 10e+9): d[x][y] = d[x-1][y]
# 윗칸, 왼쪽 칸 모두 숫자라면 윗칸+왼쪽 칸 값을 1000000007로 나눈 결과 저장
else: d[x][y] = (d[x-1][y] + d[x][y-1]) % 1000000007
# 학교 위치에 저장된 값이 x이거나 초기값이면 0, 그렇지 않으면 학교 위치에 저장된 값이 정답이다
return 0 if d[m-1][n-1] in (10e+9, 'x') else d[m-1][n-1]
예시

1번 과정에서 이중리스트 d를 초기화 한다 (빈 칸은 모두 10e+9로 초기화 되었다고 가정)
그리고 물 웅덩이 위치인 x를 표시한다.

이후 3, 4번 과정을 수행하면 위와 같은 모습이 된다.
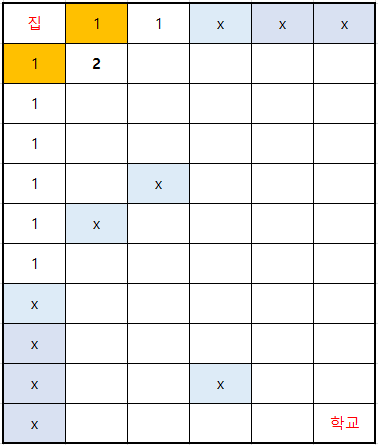
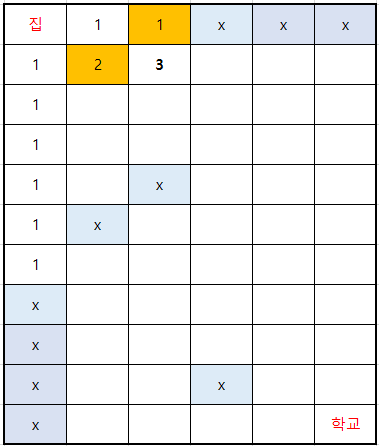
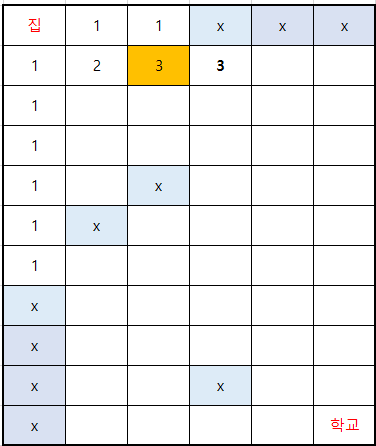
위 3개의 그림은 5번의 과정이다.
왼쪽 칸과 위쪽 칸의 수를 더해서 수가 결정되는데, 만약 둘 중 하나가 x(물 웅덩이)라면 x가 아닌 숫자를 그대로 가져간다. 이런 방식으로 쭉 진행을 하면 다음과 같은 상황도 나온다.

위와 같이 왼쪽, 위쪽 칸 모두 물 웅덩이인 경우엔 초기값이 저장된 상태로 그냥 넘어간다. 저 칸을 거쳐서 가면 최소 거리가 나오지 않는다. 물 웅덩이를 피해 저 칸을 가려면 왼쪽으로 되돌아 가거나 위쪽으로 올라가 할 수밖에 없기 때문이다.

모든 부분에 대해 계산이 완료되면 학교까지의 최단 거리 수를 구할 수 있다.


전체 코드
def solution(m, n, puddles):
answer = 0
d = [[10e+9] * n for _ in range(m)]
for puddle in puddles:
d[puddle[0]-1][puddle[1]-1] = 'x'
# 첫 열 초기화
for i in range(1, n):
if d[0][i] == 'x' or d[0][i-1] == 'x': d[0][i] = 'x'
else: d[0][i] = 1
# 첫 행 초기화
for j in range(1, m):
if d[j][0] == 'x' or d[j-1][0] == 'x': d[j][0] = 'x'
else: d[j][0] = 1
for x in range(1, m):
for y in range(1, n):
if d[x][y] == 'x' or (d[x-1][y], d[x][y-1]) == ('x','x'): continue
if d[x-1][y] in ('x', 10e+9): d[x][y] = d[x][y-1]
elif d[x][y-1] in ('x', 10e+9): d[x][y] = d[x-1][y]
else: d[x][y] = (d[x-1][y] + d[x][y-1]) % 1000000007
return 0 if d[m-1][n-1] in (10e+9, 'x') else d[m-1][n-1]
'알고리즘 > 코딩 테스트' 카테고리의 다른 글
| [프로그래머스 lv3] 2 x n 타일링 (DP 문제) (0) | 2021.10.12 |
|---|---|
| [프로그래머스 위클리 챌린지 10주차] 교점에 별 만들기 (0) | 2021.10.12 |
| [프로그래머스 lv3] 베스트앨범 (0) | 2021.10.12 |
| [프로그래머스 lv3] 하노이의 탑 (재귀 문제) (0) | 2021.10.12 |
| [프로그래머스 lv2] 쿼드압축 후 개수 세기 (queue 풀이) (0) | 2021.10.09 |
| [프로그래머스 lv2] [1차] 캐시 (최소heap 풀이) (0) | 2021.10.09 |
| [프로그래머스 lv2] [3차]압축 (0) | 2021.10.09 |
| [프로그래머스 lv2] 순위 검색 (최적화 문제) (0) | 2021.10.09 |




