라떼는말이야
[solved.ac 골드4] 1229_육각수 (파이썬, DP) 본문


문제
육각수는 육각형을 이용해 정의할 수 있다. hn은 한 변에 점 1, 2, ..., n개가 있는 육각형을 점 하나만 겹치게 그렸을 때 존재하는 서로 다른 점의 개수이다.

그림1은 h1, h2, h3, h4를 의미하며, 처음 육각수 6개는 1, 6, 15, 28, 45, 66이다.
자연수 N이 주어졌을 때, 합이 N이 되는 육각수 개수의 최솟값을 구해보자.
| N | 최소개수 | 합 |
| 1 | 1 | 1 |
| 2 | 2 | 1+1 |
| 3 | 3 | 1+1+1 |
| 4 | 4 | 1+1+1+1 |
| 5 | 5 | 1+1+1+1+1 |
| 6 | 1 | 6 |
| 7 | 2 | 1+6 |
| 8 | 3 | 1+1+6 |
| 9 | 4 | 1+1+1+6 |
| 10 | 5 | 1+1+1+1+6 |
| 11 | 6 | 1+1+1+1+1+6 |
| 12 | 2 | 6+6 |
1791보다 큰 정수는 항상 육각수 4개의 합으로 만들 수 있다. 또한, 수가 충분히 크다면 항상 육각수 3개의 합으로 만들 수 있다. 또, 최소 개수는 항상 6 이하이고, 이것이 최소인 N은 11과 26밖에 없다. 답이 6인 가장 큰 N은 26, 5인 가장 큰 N은 130, 4인 가장 큰 N은 146858이다.
입력
첫째 줄에 N이 주어진다.
출력
첫째 줄에 N을 만들기 위해 필요한 육각수 개수의 최솟값을 출력한다.
제한
- 1 ≤ N ≤ 1,000,000
예제
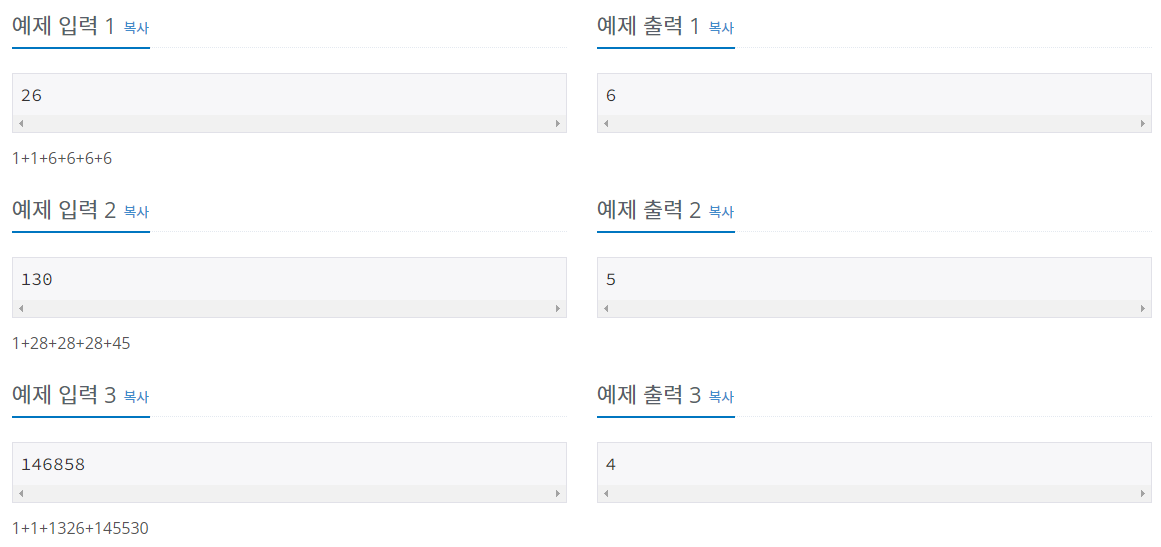
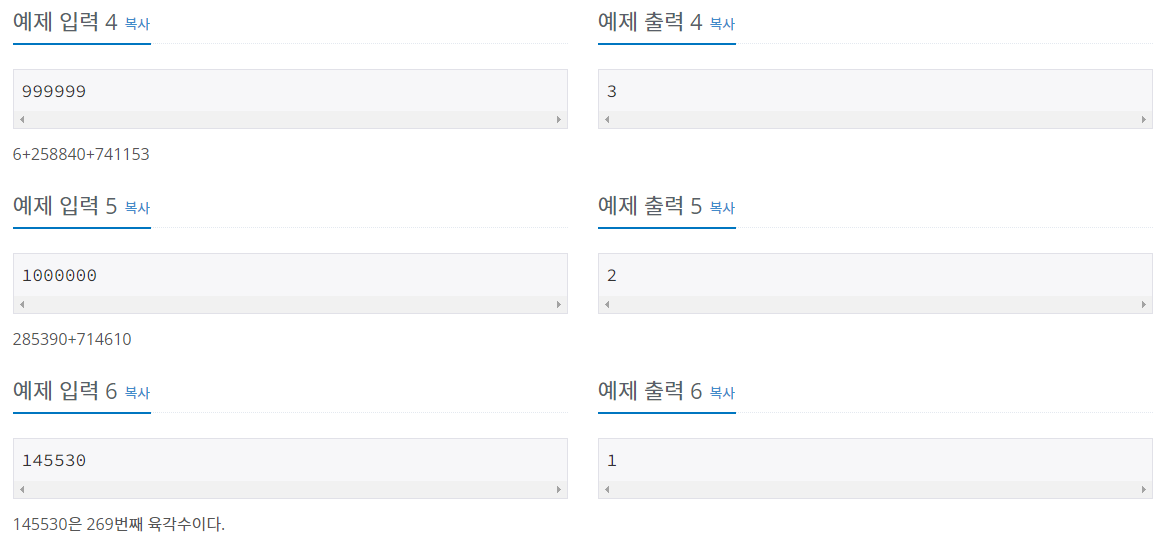
나의 풀이
우선 이 문제를 풀기 위해서는 육각수의 개수를 구하는 방법을 알아야 한다.
한 변이 n인 육각수의 점의 개수: n(2n - 1)
육각수가 규칙성 있기 늘어나기 때문에 직접 공식을 찾아도 되고, 구글링 해봐도 나온다.
우선 문제에서 제공한 힌트를 사용해 DP에 사용할 리스트 d를 생성했다. d[i]는 i를 만들 수 있는 육각수의 최소 개수이다.
INF = 10 ** 9
d = [0, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 6, 2] + [INF] * 1_000_000물론 점화식을 잘 세운다면 초기값 몇 개만으로도 문제를 풀이할 수 있고, 이 문제에서도 마찬가지이다. 0, 1 정도로만 초기화 돼도 무관하다. 하지만 문제를 풀 때 힌트를 활용했기에 풀고 나서도 그냥 유지했다.
문제에서 구하고자 하는 N보다 큰 육각수로는 N을 만들 수 없기 때문에 N보다 작은 육각수들을 찾는 함수를 작성하였다.
def get_hex(limit): # limit 이하의 육각수 구하기
n = 1
current = 0
ans = []
while current <= limit:
current = n * (2 * n - 1)
ans.append(current)
n += 1
return ans[:-1]매개 변수로 받은 limit보다 작은 육각수를 찾는다. 육각수는 위에서 적은 것과 같이 n(2n-1) 로 구하고, ans에 저장한다.
마지막 요소를 제외하고 return하는 이유는 조건 검사 후에 내부를 수행하기 때문에 마지막에 limit보다 큰 값이 들어가기 때문이다. 이를 제외한 것이다.
def solution():
n = int(input())
if n < 13:
print(d[n])
return
hex = get_hex(n)
for i in range(13, n + 1):
min_val = INF
for h in hex:
if h > i: break
min_val = min(min_val, d[i - h])
d[i] = min_val + 1
print(d[n])
n을 입력 받고, 앞서 하드 코딩으로 저장해둔 12개보다 작은 n을 찾으면 바로 출력하고 끝낸다.
우선 hex에 위에서 정의한 get_hex() 함수로 n보다 작은 육각수들을 구한다.
그리고 각 육각수 만큼을 뺀 값 중 최소 값을 찾는다.
이 부분이 잘 이해가 안 갈 수도 있는데, 예를 들어 n이 10 일 때 육각수는 1+1+1+1+1+6 으로 6개의 육각수로 표현될 수 있다. (문제에서 주어진 맞는 값이다)
육각수가 1, 6, 15, 28, 45, 66, 91 ... 이렇게 되는데 n이 11, 16, 25, 38, 55, 76, 101...(10에 육각수를 더한 값) 일 때는 n이 10일 때 최소 개수였던 6개에 1만 더해주면 된다.
- n이 11 일 때는 1+1+1+1+1+6 + 1
- n이 16 일 때는 1+1+1+1+1+6 + 6
- n이 25 일 때는 1+1+1+1+1+6 + 15
- n이 38 일 때는 1+1+1+1+1+6 + 28
- n이 55 일 때는 1+1+1+1+1+6 + 45
- n이 76 일 때는 1+1+1+1+1+6 + 66
- n이 101 일 때는 1+1+1+1+1+6 + 91
이를 반대로 이용하면 어떤 수 N이 최소 몇 개의 육각수로 이루어졌는지 알기 위해서 (N - 육각수들) 중 최소 값 + 1 으로 구할 수 있다.
이렇게 구한 d 리스트의 n번째 값이 답이 된다.
전체 코드
INF = 10 ** 9
d = [0, 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 6, 2] + [INF] * 1_000_000
def get_hex(limit): # limit 이하의 육각수 구하기
n = 1
current = 0
ans = []
while current <= limit:
current = n * (2 * n - 1)
ans.append(current)
n += 1
return ans[:-1]
def solution():
n = int(input())
if n < 13:
print(d[n])
return
hex = get_hex(n)
for i in range(13, n + 1):
min_val = INF
for h in hex:
if h > i: break
min_val = min(min_val, d[i - h])
d[i] = min_val + 1
print(d[n])
solution()

이 문제를 파이썬으로 푼 사람 14명 중 한 명이 됐다 (전체 제출 자체가 적지만...)

'알고리즘 > 코딩 테스트' 카테고리의 다른 글
| [프로그래머스 lv2] 주차 요금 계산 (파이썬, 문자열, 구현) (0) | 2022.05.04 |
|---|---|
| [solved.ac 골드5] 1501_영어 읽기 (파이썬, 문자열, 해시맵) (2) | 2022.04.24 |
| [solved.ac 실버2] 1058_친구 (파이썬, 브루트포스, 그래프) (0) | 2022.04.17 |
| [solved.ac 실버1] 16918_봄버맨 (파이썬, 그래프) (2) | 2022.04.15 |
| [solved.ac 실버2] 1890_점프 (파이썬, DP) (0) | 2022.04.13 |
| [solved.ac 실버2] 1912_연속합 (파이썬, DP) (0) | 2022.04.13 |
| [solved.ac 실버2] 11053_가장 긴 증가하는 부분 수열 (파이썬, DP) (0) | 2022.04.13 |
| [solved.ad 실버3] 2407_조합 (파이썬, DP) (0) | 2022.04.13 |




