라떼는말이야
[프로그래머스 lv2] 배달 (파이썬, 최단 거리 탐색, 다익스트라) 본문

문제 설명
N개의 마을로 이루어진 나라가 있습니다. 이 나라의 각 마을에는 1부터 N까지의 번호가 각각 하나씩 부여되어 있습니다. 각 마을은 양방향으로 통행할 수 있는 도로로 연결되어 있는데, 서로 다른 마을 간에 이동할 때는 이 도로를 지나야 합니다. 도로를 지날 때 걸리는 시간은 도로별로 다릅니다. 현재 1번 마을에 있는 음식점에서 각 마을로 음식 배달을 하려고 합니다. 각 마을로부터 음식 주문을 받으려고 하는데, N개의 마을 중에서 K 시간 이하로 배달이 가능한 마을에서만 주문을 받으려고 합니다. 다음은 N = 5, K = 3인 경우의 예시입니다.

위 그림에서 1번 마을에 있는 음식점은 [1, 2, 4, 5] 번 마을까지는 3 이하의 시간에 배달할 수 있습니다. 그러나 3번 마을까지는 3시간 이내로 배달할 수 있는 경로가 없으므로 3번 마을에서는 주문을 받지 않습니다. 따라서 1번 마을에 있는 음식점이 배달 주문을 받을 수 있는 마을은 4개가 됩니다.
마을의 개수 N, 각 마을을 연결하는 도로의 정보 road, 음식 배달이 가능한 시간 K가 매개변수로 주어질 때, 음식 주문을 받을 수 있는 마을의 개수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- 마을의 개수 N은 1 이상 50 이하의 자연수입니다.
- road의 길이(도로 정보의 개수)는 1 이상 2,000 이하입니다.
- road의 각 원소는 마을을 연결하고 있는 각 도로의 정보를 나타냅니다.
- road는 길이가 3인 배열이며, 순서대로 (a, b, c)를 나타냅니다.
- a, b(1 ≤ a, b ≤ N, a != b)는 도로가 연결하는 두 마을의 번호이며, c(1 ≤ c ≤ 10,000, c는 자연수)는 도로를 지나는데 걸리는 시간입니다.
- 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있습니다.
- 한 도로의 정보가 여러 번 중복해서 주어지지 않습니다.
- K는 음식 배달이 가능한 시간을 나타내며, 1 이상 500,000 이하입니다.
- 임의의 두 마을간에 항상 이동 가능한 경로가 존재합니다.
- 1번 마을에 있는 음식점이 K 이하의 시간에 배달이 가능한 마을의 개수를 return 하면 됩니다.
입출력 예
| N | road | K | result |
| 5 | [[1,2,1],[2,3,3],[5,2,2],[1,4,2],[5,3,1],[5,4,2]] | 3 | 4 |
| 6 | [[1,2,1],[1,3,2],[2,3,2],[3,4,3],[3,5,2],[3,5,3],[5,6,1]] | 4 | 4 |
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
주어진 마을과 도로의 모양은 아래 그림과 같습니다.

1번 마을에서 배달에 4시간 이하가 걸리는 마을은 [1, 2, 3, 5] 4개이므로 4를 return 합니다.
나의 풀이
어떤 지점에서 다른 모든 지점까지의 최소 거리를 구하는 대표적인 알고리즘으로 다익스트라(Dijkstra) 알고리즘이 있다. 나는 이 문제를 우선 순위 큐(with Heap)를 사용한 다익스트라 알고리즘을 활용해 풀었다.
다익스트라 알고리즘
import heapq
INF = 10**9 # 충분히 큰 값
distance, graph = list(), list()
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist: continue
for t, d in graph[now].items():
cost = dist + d
if cost < distance[t]:
distance[t] = cost
heapq.heappush(q, (cost, t))이 글에서 다익스트라 알고리즘에 대해 설명하지는 않을 것이다. 다익스트라 알고리즘에 대해 잘 모른다면 구글에 굉장히 다양한 설명이 있으니 참고하면 될 듯 하다.
힙을 사용한 우선 순위 큐로 시간 복잡도를 줄였다. 파이썬의 heapq는 최소 힙을 표현할 수 있는데 힙에 튜플이나 리스트가 들어가 있다면 첫 번째 요소를 비교한 뒤 첫 번째 요소가 같다면 그 다음 요소를 확인하는 방식으로 크기를 비교한다.
현재 방문 중인 노드와 연결 된 노드 중 거리가 가장 짧은 것을 고르기 위해 힙에 push 할 때는 (거리, 노드) 와 같이 거리가 첫 번째 요소로 오도록 push했다.
최단 거리를 찾을 때마다 전역 변수로 선언된 distance의 값을 수정한다.
메인 함수
INF = 10**9 # 충분히 큰 값
distance, graph = list(), list()
def dijkstra():
# ... 위에서 설명
pass
def solution(N, road, K):
global distance, graph
# 거리 무한대로 초기화
distance = [INF] * (1 + N)
# 그래프에 a -> b , b -> a 최단 거리 추가
graph = [dict() for _ in range(N + 1)]
for _from, _to, dist in road:
# a -> b
if _to in graph[_from].keys():
graph[_from][_to] = min(graph[_from][_to], dist)
else:
graph[_from][_to] = dist
# b -> a
if _from in graph[_to].keys():
graph[_to][_from] = min(graph[_to][_from], dist)
else:
graph[_to][_from] = dist
# 최단 경로 찾기
dijkstra(1)
return len([d for d in distance if d <= K])메인 함수인 solution()에서는 distance에 모든 노드까지의 거리를 무한대로 설정한다. (문제에서 노드가 1부터 시작하기 때문에 N + 1 크기로 선언해서 인덱스를 그대로 사용할 수 있도록 했다)
그리고 graph에는 각 인덱스마다 사전으로 초기화했다.
만약 3번 노트에 1, 2, 4번 노드가 연결되어 있다면 graph[3]에는 {1: ??, 2: ??, 4: ??} 가 저장되어 있을 것이다. 제한 사항에서 두 마을 a, b를 연결하는 도로는 여러 개가 있을 수 있다고 했기 때문에 그 도로 중 최소 값을 찾아서 갱신하기 위해 찾아야하는데 그냥 리스트로 저장해서 선형적으로 찾는 것보다 사전을 사용하면 O(1) 복잡도로 찾을 수 있기 때문에 사전에 정보를 저장하는 방식을 선택했다.
마을은 단방향 그래프가 아닌 양방향이므로 a -> b 로 가는 경우와 b -> a 로 가는 경우를 모두 저장해야 한다.
dijkstra(1)를 수행하면 1번 노드에서 나머지 노드까지 갈 수 있는 최단 거리가 distance 리스트에 저장된다.
마지막으로 거리가 K보다 작거나 같은 마을의 개수를 return하면 된다.
전체 코드
import heapq
INF = 10**9 # 충분히 큰 값
distance, graph = list(), list()
def dijkstra(start):
q = []
heapq.heappush(q, (0, start))
distance[start] = 0
while q:
dist, now = heapq.heappop(q)
if distance[now] < dist: continue
for t, d in graph[now].items():
cost = dist + d
if cost < distance[t]:
distance[t] = cost
heapq.heappush(q, (cost, t))
def solution(N, road, K):
global distance, graph
# 거리 무한대로 초기화
distance = [INF] * (1 + N)
# 그래프에 a -> b , b -> a 최단 거리 추가
graph = [dict() for _ in range(N + 1)]
for _from, _to, dist in road:
# a -> b
if _to in graph[_from].keys():
graph[_from][_to] = min(graph[_from][_to], dist)
else:
graph[_from][_to] = dist
# b -> a
if _from in graph[_to].keys():
graph[_to][_from] = min(graph[_to][_from], dist)
else:
graph[_to][_from] = dist
# 최단 경로 찾기
dijkstra(1)
return len([d for d in distance if d <= K])
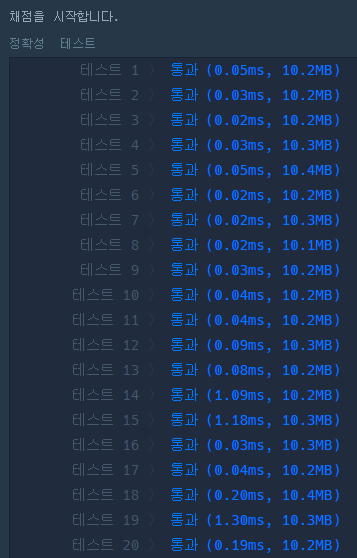
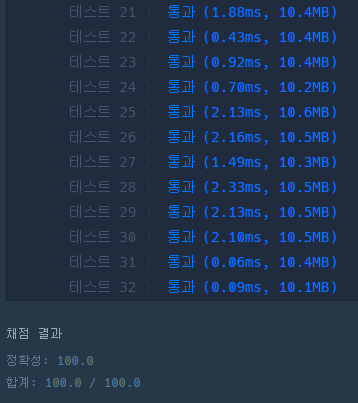
'알고리즘 > 코딩 테스트' 카테고리의 다른 글
| [solved.ac 골드3] 16236_아기 상어 (파이썬, 구현, BFS) (0) | 2022.05.19 |
|---|---|
| [solved.ac 골드5] 1351_무한 수열 (파이썬, 재귀, 자료 구조, DP) (0) | 2022.05.16 |
| [solved.ac 실버1] 1553_도미노 찾기 (파이썬, 백트래킹) (0) | 2022.05.13 |
| [프로그래머스 lv3] 표 편집 (파이썬, 문자열, LinkedList) (0) | 2022.05.06 |
| [프로그래머스 lv2] 주차 요금 계산 (파이썬, 문자열, 구현) (0) | 2022.05.04 |
| [solved.ac 골드5] 1501_영어 읽기 (파이썬, 문자열, 해시맵) (2) | 2022.04.24 |
| [solved.ac 실버2] 1058_친구 (파이썬, 브루트포스, 그래프) (0) | 2022.04.17 |
| [solved.ac 실버1] 16918_봄버맨 (파이썬, 그래프) (2) | 2022.04.15 |




