라떼는말이야
[solved.ac 실버1] 1553_도미노 찾기 (파이썬, 백트래킹) 본문


문제

도미노의 크기는 1×2이고, 크기가 1×1인 칸으로 나누어져 있다. 칸은 수를 나타내며, 위와 같이 총 28가지가 있다.
크기가 8×7인 격자가 있고, 격자의 각 칸에는 정수가 하나씩 들어있다. 위의 도미노를 이용해 문제의 격자와 같은 상태를 만드는 방법의 수를 구해보자.
격자의 칸에 적힌 수는 도미노의 칸이 의미하는 수와 같아야 한다. 도미노는 회전할 수 있으며, 같은 도미노를 여러 번 사용하면 안된다.
입력
총 8개의 줄에 격자의 상태가 주어진다. 격자에는 0부터 6까지의 수만 존재한다.
출력
첫째 줄에 경우의 수를 출력한다.
예제

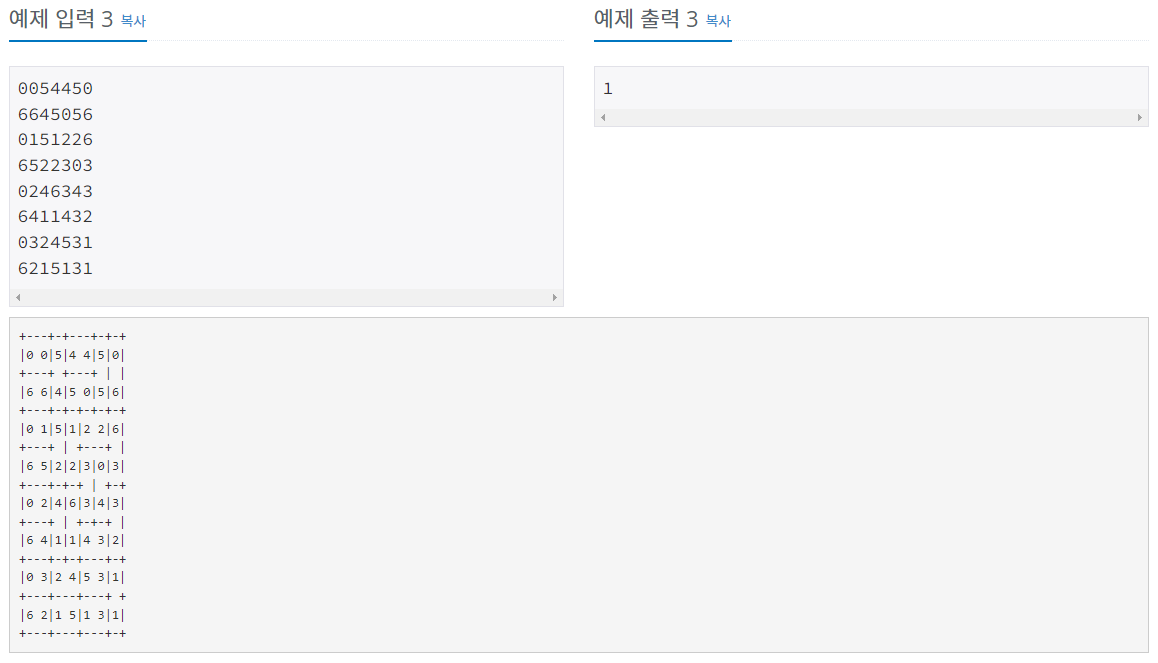
나의 풀이
이 문제는 백트래킹을 이용한 완전 탐색으로 풀이했다.
도미노는 ㅡ(가로)나 |(세로) 로 놓을 수 있다. 어떤 칸을 정하고 그 오른쪽을 선택하면 가로, 그 밑을 선택하면 세로로 놓은 것이 된다.
백트래킹은 재귀 호출을 활용하기 때문에 탈출 조건이 필요하다. 탈출 조건은 8 x 7의 격자를 모두 탐색한 후에 탈출하면 된다. x의 인덱스가 8이 된 순간 1을 return한다. 여기서 1이 의미하는 것은 끝까지 탐색하면서 도미노를 놓을 수 있는 경우를 하나 찾았다는 것이다.
도미노를 놓을 때 2가지를 확인해야 한다.
- 놓으려는 위치가 비어있는지 (visited 리스트 사용)
- 아직 사용하지 않은 도미노인지 (domino 리스트 사용)
우선 완료 조건과 다음으로 이동하는 부분을 보면 다음과 같다
graph = [list(map(int, list(input()))) for _ in range(8)]
visited = [[False] * 7 for _ in range(8)]
domino = [[False] * 7 for _ in range(7)]
def rec_fun(x, y):
if x == 8: return 1 # 탐색 완료
count = 0
nx, ny = x, y + 1 # 오른쪽으로 이동
if ny == 7: # 오른쪽 끝이라면 개행
nx, ny = x + 1, 0
if visited[x][y]:
return rec_fun(nx, ny) # 다음 위치로 이동graph에 격자를 입력 받고, visited는 graph의 크기인 8 x 7 크기로, domino는 00~66까지 존재하므로 7 x 7 크기의 리스트로 만들었다.
도미노를 보면 뒤집었을 때 같은 모양이 나오지 않는다. 예를 들어 3,5와 5,3이 중복되지 않는다. 그래서 사용한 도미노를 체크할 때 3,5를 사용했다면 domino[3][5] = True와 domino[5][3] = True와 같이 처리해주어야 한다.
위에서 설명한 x가 8이 되면(탐색이 완료되면) 1을 리턴하는 부분이 있고, 전체 개수를 세기 위한 count 변수가 있다.
nx, ny는 다음으로 탐색할 위치이다. 기본적으로 오른쪽으로 이동하지만 현재 오른쪽 끝에 다다랐다면 개행을 해서 탐색하는 모습이다.
현재 위치를 방문했다는 것은 이미 도미노가 놓여졌다는 의미이므로 다음 위치로 이동한다.
다음은 현재 위치에 아직 도미노가 놓여지지 않은 경우의 처리이다.
# ...
else:
now = graph[x][y]
visited[x][y] = True
for dx, dy in ((0, 1), (1, 0)): # 오른쪽, 아래 확인
mx, my = x + dx, y + dy
if mx in range(8) and my in range(7):
pair = graph[mx][my] # 오른쪽이나 아래 값
if not visited[mx][my] and not domino[now][pair]: # 놓을 수 있고, 사용되지 않은 도미노
domino[now][pair] = domino[pair][now] = True
visited[mx][my] = True
count += rec_fun(nx, ny) # 다음 위치로 이동
visited[mx][my] = False
domino[now][pair] = domino[pair][now] = False
visited[x][y] = False
return count현재 위치의 값을 now로 놓고 현재 위치를 방문처리한다. now를 사용해 놓을 수 있는 도미노를 확인할 것이다.
그리고 오른쪽과 아래를 확인한다. 도미노를 가로로 놓거나 세로로 놓는 과정이다.
설명하기 편하게 도미노를 이루고 있는 2개의 블록 중 현재 위치에 놓을 블록을 메인 블록, 메인 블록에서 오른쪽이나 아래에 놓을 블록을 서브 블록이라고 하겠다.
mx, my는 서브 블록의 위치이다. 서브 블록의 위치를 확인해서 격자를 벗어나지 않았다면 다음 과정을 진행할 수 있다.
pair에는 서브 블록의 값을 저장한다. (앞서 구한 now와 결합하면 현재 위치에서 사용해야 할 도미노를 알 수 있다)
서브 블록(mx, my)를 놓을 수 있는지 visited로 확인하고, now와 pair를 결합해 domino로 사용된 도미노인지 확인한다.
블록을 놓을 수 있고, 아직 사용하지 않은 도미노라면 도미노를 사용 처리하고, 방문 처리한다. 이때 도미노는 domino[now][pair]와 domino[pair][now] 둘 다 True로 사용 처리 한다.
도미노를 놓았다면 위에서 구했던 다음 위치(nx, ny)로 이동한다.
이동하고 돌아와서는 visited와 domino를 사용한 것을 다시 False로 설정해주어서 백트래킹 할 수 있도록 한다.
현재 위치 탐색이 완료 되었다면 마찬가지로 현재 위치에 대한 visited를 False로 설정해준다.
일련의 과정이 완료되면 count에는 도미노를 놓을 수 있는 경우의 수가 저장되어 있을 것이다.
전체 코드
graph = [list(map(int, list(input()))) for _ in range(8)]
visited = [[False] * 7 for _ in range(8)]
domino = [[False] * 7 for _ in range(7)]
def rec_fun(x, y):
if x == 8: return 1 # 탐색 완료
count = 0
nx, ny = x, y + 1 # 오른쪽으로 이동
if ny == 7: # 오른쪽 끝이라면 개행
nx, ny = x + 1, 0
if visited[x][y]:
return rec_fun(nx, ny) # 다음 위치로 이동
else:
now = graph[x][y]
visited[x][y] = True
for dx, dy in ((0, 1), (1, 0)): # 오른쪽, 아래 확인
mx, my = x + dx, y + dy
if mx in range(8) and my in range(7):
pair = graph[mx][my] # 오른쪽이나 아래 값
if not visited[mx][my] and not domino[now][pair]: # 놓을 수 있고, 사용되지 않은 도미노
domino[now][pair] = domino[pair][now] = True
visited[mx][my] = True
count += rec_fun(nx, ny) # 다음 위치로 이동
visited[mx][my] = False
domino[now][pair] = domino[pair][now] = False
visited[x][y] = False
return count
print(rec_fun(0, 0)) # start
'알고리즘 > 코딩 테스트' 카테고리의 다른 글
| [solve.ac] 16928_뱀과 사다리 게임 (파이썬, BFS) (0) | 2022.05.21 |
|---|---|
| [solved.ac 실버1] 1149_RGB 거리 (파이썬, DP 풀이) (0) | 2022.05.21 |
| [solved.ac 골드3] 16236_아기 상어 (파이썬, 구현, BFS) (0) | 2022.05.19 |
| [solved.ac 골드5] 1351_무한 수열 (파이썬, 재귀, 자료 구조, DP) (0) | 2022.05.16 |
| [프로그래머스 lv3] 표 편집 (파이썬, 문자열, LinkedList) (0) | 2022.05.06 |
| [프로그래머스 lv2] 배달 (파이썬, 최단 거리 탐색, 다익스트라) (0) | 2022.05.05 |
| [프로그래머스 lv2] 주차 요금 계산 (파이썬, 문자열, 구현) (0) | 2022.05.04 |
| [solved.ac 골드5] 1501_영어 읽기 (파이썬, 문자열, 해시맵) (2) | 2022.04.24 |




