라떼는말이야
[solved.ac 골드3] 2437_저울 (그리디, 파이썬, 코틀린) 본문
https://github.com/mangbaam/CodingTest
GitHub - mangbaam/CodingTest: 프로그래머스, 백준 등 코딩테스트 풀이를 기록하는 저장소입니다.
프로그래머스, 백준 등 코딩테스트 풀이를 기록하는 저장소입니다. Contribute to mangbaam/CodingTest development by creating an account on GitHub.
github.com
밑의 사진을 클릭하면 문제 링크로 이동합니다


문제
하나의 양팔 저울을 이용하여 물건의 무게를 측정하려고 한다. 이 저울의 양 팔의 끝에는 물건이나 추를 올려놓는 접시가 달려 있고, 양팔의 길이는 같다. 또한, 저울의 한쪽에는 저울추들만 놓을 수 있고, 다른 쪽에는 무게를 측정하려는 물건만 올려놓을 수 있다.

무게가 양의 정수인 N개의 저울추가 주어질 때, 이 추들을 사용하여 측정할 수 없는 양의 정수 무게 중 최솟값을 구하는 프로그램을 작성하시오.
예를 들어, 무게가 각각 3, 1, 6, 2, 7, 30, 1인 7개의 저울추가 주어졌을 때, 이 추들로 측정할 수 없는 양의 정수 무게 중 최솟값은 21이다.
입력
첫 째 줄에는 저울추의 개수를 나타내는 양의 정수 N이 주어진다. N은 1 이상 1,000 이하이다. 둘째 줄에는 저울추의 무게를 나타내는 N개의 양의 정수가 빈칸을 사이에 두고 주어진다. 각 추의 무게는 1이상 1,000,000 이하이다.
출력
첫째 줄에 주어진 추들로 측정할 수 없는 양의 정수 무게 중 최솟값을 출력한다.
예제

나의 풀이
이것 저것 여러 시도를 해보다가 코드를 정리하다보니 결국 짧은 코드로 풀이할 수 있었다.
코틀린을 연습하기 위해 코틀린으로 먼저 풀어봤고, 파이썬이 익숙한 사람이 훨씬 많을 듯 해서 파이썬으로도 풀이해보았다.
문제의 예제를 활용해보도록 하겠다.
1. 정렬한다
1 1 2 3 6 7 30
2. 각 무게를 순회하며 해당 무게를 포함해 더 가벼운 추들로 만들 수 있는 무게들을 생각해보자.
- [1] - 1
- [1, 1] - 1, 2
- [1, 1, 2] - 1, 2, 3, 4
- [1, 1, 2, 3] - 1, 2, 3, 4, 5, 6, 7
- ...
3. 규칙을 찾아보자
만약 [1, 1, 2] 에서 1, 2, 3, 4 를 만들 수 있다는 사실을 알고 있을 때 거기에 3을 추가해서 [1, 1, 2, 3] 으로 만들 수 있는 무게들은 기존의 [1, 1, 2] 로 만들 수 있는 1, 2, 3, 4 와 각각의 숫자에 3을 더해서 만들 수 있는 3, 4, 5, 6, 7 을 추가로 만들 수 있다. 그래서 결국 1, 2, 3, 4, 5, 6, 7 을 만들 수 있는 것이다. (3, 4를 만들 수 있는 경우의 수는 2개인 것이다)
4. 규칙에 따라 처음부터 확인해보자
- [1] - 1을 만들 수 있다
- [1, 1] - [1] 로 만들 수 있는 (1) 에 1을 추가해 1, 2를 추가로 만들 수 있다. 결국 1, 2를 만들 수 있다
- [1, 1, 2] - [1, 1] 로 만들 수 있는 (1, 2) 에 2를 추가해 2, 3, 4 를 추가로 만들 수 있다. 결국 1, 2, 3, 4 를 만들 수 있다
- [1, 1, 2, 3] - [1, 1, 2] 로 만들 수 있는 (1, 2, 3, 4) 에 3을 추가해 3, 4, 5, 6, 7 을 추가로 만들 수 있다. 결국 1, 2, 3, 4, 5, 6, 7 을 만들 수 있다
- ...
- 결국 이전 무게들로 만들 수 있는 연속된 무게들에 새로 추가되는 무게만큼 더한 숫자들이 현재 만들 수 있는 무게들이다.
5. 연속되는 숫자인지 확인해보자
4번의 규칙에 따라 무게를 찾아보면 정렬된 무게들 중 i - 1 까지의 무게로 만들 수 있는 연속된 무게들과 i 를 추가했을 때 i - 1 까지의 무게에 i 번째 무게를 더해서 만들어질 새로 추가될 무게들로 나누어 생각해볼 수 있다.
4번에서 [1, 1, 2, 3] 까지 확인했는데 이어서 쭉 확인해보자
- [1, 1, 2, 3, 6] - [1, 1, 2, 3] 으로 만들 수 있는 (1 ~ 7) + [6] 을 더해서 만들 수 있는 (6 ~ 13) 를 합치면 (1 ~ 13) 의 연속된 무게를 만들 수 있다
- [1, 1, 2, 3, 6, 7] - [1, 1, 2, 3, 6] 으로 만들 수 있는 (1 ~ 13) + [7] 을 더해서 만들 수 있는 (7 ~ 20) 을 합치면 (1 ~ 20) 의 연속된 무게를 만들 수 있다
- [1, 1, 2, 3, 6, 7, 30] - [1, 1, 2, 3, 6, 7] 로 만들 수 있는 (1 ~ 20) + [30] 을 더해서 만들 수 있는 (30 ~ 50) 을 합치면 (1 ~ 20, 30 ~ 50) 의 무게를 만들 수 있다
- 여기서 21 ~ 29 까지의 무게를 만들 수 없다는 사실을 알 수 있다. 즉, 가장 작은 값인 21 이 답이 된다.
6. 간단하게 생각해보자
입력 받은 무게들을 정렬했을 때 [ ..., 20, 30, ... ] 이고, 20까지의 무게로 만들 수 있는 무게들이 연속적이라고 했을 때 30을 추가하게 되면 30부터 (20까지 무게로 만들 수 있는 무게 중 가장 무거운 무게 + 30) 이 추가로 만들 수 있는 무게이다.
이때 (20까지 무게로 만들 수 있는 무게 중 가장 무거운 무게) 와 30이 겹쳐야 한다.
(이전 무게들로 만들 수 있는 무게 중 가장 무거운 무게) >= (새로 추가될 무게)
위 공식이 성립이 되어야 연속된 무게를 만들 수 있다.
반대로 말하면 위 공식이 성립이 되지 않는 순간에 새로 추가될 무게가 정답이 된다는 말이다.
7. 코드로 풀어보자
장황한 설명을 다 이해하는 것보다 코드로 보는 것이 훨씬 편할 수 있다.
코틀린

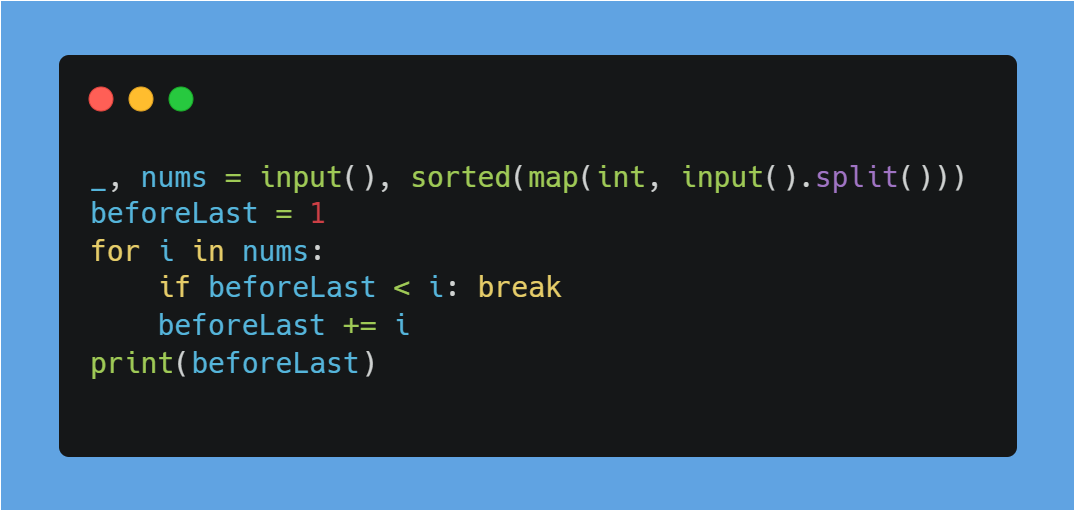
파이썬

'알고리즘 > 코딩 테스트' 카테고리의 다른 글
| [프로그래머스 lv3] 가장 먼 노드 (다익스트라, 코틀린) (0) | 2022.08.18 |
|---|---|
| [solved.ac 골드5] 17396_백도어 (다익스트라, 코틀린) (0) | 2022.08.16 |
| [solved.ac 실버2] 18352_특정 거리의 도시 찾기 (다익스트라, 코틀린) (0) | 2022.08.16 |
| 코틀린 다익스트라 알고리즘 Kotlin dijkstra algorithm (0) | 2022.08.16 |
| [solved.ac 실버3] 2992_크면서 작은 수 (파이썬, 순열) (0) | 2022.07.17 |
| [solved.ac 실버1] 1189_컴백홈 (파이썬, 브루트포스, 백트래킹) (0) | 2022.07.15 |
| [solved.ac 골드4] 1430_공격 (파이썬, BFS) (0) | 2022.07.12 |
| [solved.ac 실버3] 1515_수 이어 쓰기 (파이썬, 문자열, 브루트포스) (0) | 2022.07.09 |




